matematicas #1: 2015

sábado, 23 de mayo de 2015

5.6 Elasticidades: elasticidad de la demanda y elasticidad del ingreso

ELASTICIDAD INGRESO DE LA DEMANDA

La elasticidad ingreso de la demanda , llamada a veces elasticidad demanda-renta, mide cómo afectan las variaciones de la renta o ingresos de los consumidores a la cantidad demandada de un bien. El coeficiente de elasticidad ingreso de la demanda e I se calcula dividiendo la variación porcentual de la demanda por la variación porcentual de la renta.

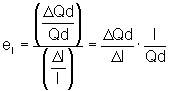
De acuerdo al valor de e I , los bienes se pueden clasificar como:

• Bienes normales : Son aquellos cuyo coeficiente de elasticidad ingreso es positivo. Esto significa que cuando aumentan los ingresos del consumidor, la demanda de los bienes normales también aumenta. Pueden ser:

• Bienes de lujo: Su coeficiente de elasticidad ingreso es mayor que 1. Es decir, cuando los ingresos del consumidor aumentan, la demanda crece en una proporción mayor.

• Bienes básicos: Su coeficiente de elasticidad ingreso es positivo y menor que 1. Es decir, cuando los ingresos del consumidor aumentan, la demanda crece en una proporción menor.

• Bienes inferiores : Su coeficiente de elasticidad ingreso es negativo. Por tanto, cuando los ingresos del consumidor aumentan, la demanda de estos bienes disminuye porque el consumidor puede optar por otros productos de mayor calidad.

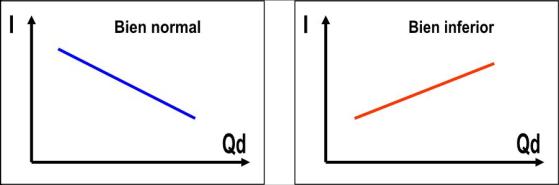
Debido a la variabilidad de la elasticidad ingreso, un bien puede ser de lujo a niveles bajos de ingreso y un bien inferior a niveles altos de ingreso.

ELASTICIDAD CRUZADA DE LA DEMANDA

La elasticidad cruzada de la demanda mide cómo evoluciona y se modifica la demanda de un bien cuando cambia el precio de otro. La elasticidad cruzada se calcula dividiendo el cambio porcentual de la cantidad demandada del bien X ante una variación porcentual del precio del bienY . Si los bienes son sustitutivos (por ejemplo, distintas marcas de automóviles) el aumento del precio de la marca X puede aumentar las ventas de la marca Y , por lo que la elasticidad cruzada será positiva. Si los bienes son complementarios, por ejemplo, los ordenadores o computadoras y el software, el aumento del precio de uno disminuirá las ventas del otro, por lo que la elasticidad cruzada será negativa. Si los bienes son independientes, por ejemplo, teléfonos y cepillos de dientes, por mucho que aumente el precio de uno no variará la demanda del otro, por lo que la elasticidad cruzada será cero.

El coeficiente de elasticidad cruzada del bien X con respecto al bien Y se define como:

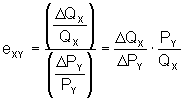
ELASTICIDAD PRECIO DE LA OFERTA

La elasticidad precio de la oferta mide cómo la variación del precio de un bien afecta a la cantidad ofrecida de ese bien, cuando todos los demás factores permanecen constantes. Se calcula dividiendo el cambio porcentual en la cantidad ofrecida por el cambio porcentual del precio.

El coeficiente de la elasticidad precio de la oferta ( e O ) es una medida del cambio porcentual de la cantidad ofrecida de un artículo por unidad de tiempo, que resulta de una variación porcentual del precio del artículo. Si ?Qo representa el cambio en la cantidad ofrecida de un artículo debido a un cambio en su precio ?P, el coeficiente de elasticidad se define como:

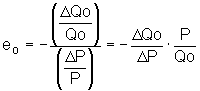
De acuerdo a este criterio, la oferta se puede clasificar en elástica (si e O > 1), inelástica (si e O < 1) y unitaria (si e O = 1). Se pueden encontrar e O arco y e O punto de la misma forma que e arco y e punto.

http://www.aulafacil.com/cursosenviados/cursomicroeconomia/Lecc-7.htm

5.5 Optimización de funciones económico - administrativas: maximización de funciones de ingreso, utilidad y beneficios: minimización de funciones de costos y de costos promedio.

http://es.slideshare.net/nelfabyes/funcion-costo-promedio

5.4 Concavidad, puntos de inflexión y prueba y prueba de la segunda derivada.

El criterio de la segunda derivada proporciona la concavidad de una curva de la siguiente manera.

a) Puntos críticos.
b) Valores máximos y mínimos.
c) Punto de inflexión.
d) La gráfica de la función.

f(x) = 3x^2 + 5x - 2

a) Puntos críticos:
f'(x)6x + 5 = 0
x = -5/6
x = -0.83

- Para obtener el punto crítico se debe de despejar la "x" en la primera derivada.
- Para obtener la segunda derivada se debe de sacar la segunda derivada y despejar la "x" si es el caso.
- La concavidad se puede deducir dependiendo del resultado de la segunda derivada. Si es positivo la concavidad estará feliz. Si es negativo la concavidad estará triste.
- El resultado también depende de la segunda derivada, si aumenta dependiendo del punto crítico, es mínimo, si disminuye dependiendo del punto crítico entonces será máximo.

c) PUNTO DE INFLEXIÓN:
- Igualar la segunda derivada con cero (0). (en este caso no hay punto de inflexión)

d) GRÁFICA:
- Sustituyes en la función original el punto crítico.(hay casos en que son dos puntos críticos)
- Sustituyes en la función original el punto de inflexión.
- Gráficas.

http://profecarlinis.galeon.com/album1608406.html

5.3 Prueba de la primera derivada para la determinación de máximos y minimos

Se llama Criterio de la primera derivada al método o teorema utilizado frecuentemente en el cálculo matemático para determinar los mínimos y máximos relativos que pueden existir en una función mediante el uso de la primera derivada o derivada principal, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto crítico

c

"Sea $c$ un punto crítico de una función $f$ que es continua en un intervalo abierto $I$ que contiene a $c$ . Si $f$ es derivable en el intervalo, excepto posiblemente en $c$ , entonces $f(c)$ puede clasificarse como sigue."

1. Si

f

(x)

cambia de positiva a negativa en

c

, entonces

f

tiene un máximo relativo en

(c, f(c))

2. Si

f

(x)

cambia de negativa a positiva en

c

, entonces

f

tiene un mínimo relativo en

(c, f(c))

3. Si

f

(x)

es positiva en ambos lados de

c

o negativa en ambos lados de c, entonces

f(c)

no es ni un mínimo ni un máximo relativo.

http://es.wikipedia.org/wiki/Criterio_de_la_primera_derivada

5.2 Extremos relativos y extremos absolutos

Máximo absoluto

Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.

Mínimo absoluto

Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.

a = 0

b = 0

Máximo y mínimo relativo

Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.

Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.

a = 3.08 b = -3.08

http://www.vitutor.com/fun/2/a_9.html

5.1 Funcion Creciente & Decreciente

FUNCIÓN CRECIENTE Y DECRECIENTE

· Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x₁y x₂, con la condición x₁ £ x₂, se verifica que

f( x₁ ) < f( x₂ ).

Se dice estrictamente creciente si de x₁ < x₂ se deduce que f(x₁) < f(x₂).

· Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x₁y x₂, que cumplan x₁ £ x₂, entonces f(x₁ ) ³ f(x₂ ).

Siempre que de x₁< x₂se deduzca f(x₁) > f(x₂), la función se dice estrictamente decreciente.

FUNC. CREC. Y DECREC. EN PUNTO

· Una función es creciente en un punto a si existe un intervalo abierto

f(x) £ f(a) si x pertenece a (a - e, a) y

f(x) ³ f(a) si x pertenece a (a, a + e).

· Análogamente, una función es decreciente en un punto a si existe un intervalo abierto (a - e, a + e) en el que

f(x) ³ f(a) si x pertenece a (a - e, a) y

f(x) £ f(a) si x pertenece a (a, a + e).

La definición de función estrictamente creciente o decreciente en un punto se obtiene sin más que sustituir el símbolo £ por < y el ³ por el >.

Es preciso diferenciar el significado de función creciente o decreciente en un intervalo del de función creciente o decreciente en un punto.

Ejemplo: estudio del crecimiento y decrecimiento de una función

-------------------------------------------------------------------------------------------------------------------------

Estudiar el crecimiento y decrecimiento de la función y = x² en los puntos

Resolución:

· La función y = x² es estrictamente creciente en el intervalo [0, +¥) puesto que si

Por otro lado, es estrictamente decreciente en (-¥, 0] ya que en este intervalo (al ser números negativos), si x₃ < x₄ Þ x₃² > x₄²(por ejemplo, -7 < -3 y (-7)² > (-3)²). Es estrictamente decreciente en x = 0.

· Nótese cómo en x = 0 la función no es creciente ni decreciente. A la izquierda de este punto es decreciente y a la derecha es creciente.

Como pone de manifiesto este ejemplo, toda función creciente en un intervalo (respectivamente decreciente) es creciente (respectivamente decreciente) en todo punto de ese intervalo.

Recíprocamente, toda función estrictamente creciente (respectivamente decreciente) en todo punto de un intervalo, es creciente (respectivamente decreciente) en todo el intervalo.

http://www.sectormatematica.cl/contenidos/funcreyd.htm

UNIDAD V. Aplicaciónes de la derivada

OBJETIVO: El alumno analizará el comportamiento de las funciones con el uso de técnicas de optimización. Aplicará estas técnicas en la resolución de problemas de las disciplinas económico-administrativas.

4.7 Aplicaciones alas ciencias económico administrativas: costo marginal, ingreso marginal, utilidad marginal, propensión marginal al consumo y propensión marginal al ahorro.

La utilidad, en microeconomía, es una medida de la satisfacción de una persona al consumir un bien o servicio. La utilidad de una persona aumenta cuando el bienestar de esa persona aumenta, y disminuye cuando su bienestar disminuye.

Si bien la utilidad es un concepto subjetivo que no se puede medir, es posible simularla utilizando funciones de utilidad, que relacionan la "cantidad" de utilidad con la cantidad consumida de ciertos bienes o servicios. Esta medida de utilidad se denomina utilidad "cardinal".

\[ U(x) = f(x) \]

En el siguiente gráfico, vemos un ejemplo de una función de utilidad:

La utilidad marginal se define, en términos discretos, como la utilidad que brinda el consumo de un bien adicional. En términos continuos, se define como la derivada parcial de la función de utilidad con respecto a la cantidad consumida de un bien.

\[ UMg(x) = \frac {dU(x)}{dx} \]

La utilidad marginal de la función de utilidad graficada anteriormente, se describe en el siguiente gráfico (La utilidad marginal en linea roja):

http://www.econlink.com.ar/utilidad/marginal

Función de consumo (C): muestra la relación entre el nivel de gasto de consumo y el nivel de renta personal disponible.

El consumo es C = Co+bY, donde Co es el consumo independiente del nivel de renta y b es el incremento que tiene esta función por cada peso adicional de renta, que además en la pendiente de la recta que representa a la función de consumo .

Propensión marginal a consumir (PMC): es la cantidad adicional que consumen los individuos cuando reciben un peso adicional de renta.

PMC= C’= (Co+bY)’= b

Función de ahorro (S): muestra la relación entre el nivel de ahorro y la renta. Del supuesto de que la renta es igual al consumo más al ahorro, se obtiene que

S= (Co)+(1-b)Y.

Propensión marginal a ahorrar (PMA): es la cantidad adicional que ahorran los individuos por cada dólar de renta adicional de renta que reciben.

PMA = S’= [ (Co)+(1-b)Y ] ‘ = 1-b =a

-Relación entre PMC y PMA:

Cada dólar adicional de renta pasa a incrementar el consumo o el ahorro. Combinando estos hechos, se calcula la PMC y la PMA: a+b = 1

Ejemplo 22 (Aplicación de la derivada de funciones de una variable)

En una economía con solo dos sectores: empresas y domésticos, la función de consumo se comporta según la expresión C = 40+0.6Y.

a-) Determine la PMC. Explique su significado.

b-) Si la función de ahorro está dada por la expresión S= (40)+0.4Y. Determine la PMA.

Solución:

a-) PMC = C’

PMC = (40+0.6Y)’

PMC = 0.6

Rta: Los sectores de la economía dedican $0.6 al consumo por cada peso adicional de renta.

b-) PMA = S’

PMA = [(40)+0.4Y]’

PMA = 0.4

Rta: Dedican al ahorro $0.4 por cada peso adicional de renta.

Ejemplo 23 (Aplicación de la integral indefinida)

La propensión marginal al ahorro es S’(Y) = 1-1/2Y-1/3. El ahorro total es cero cuando el ingreso es 8.

a-) Hallar la función de ahorro.

Solución

S(Y) = ∫ S´(Y) * dY

= ∫ (1-1/2Y-1/3) dY

= Y –3 √³Y2 + C

S(8) = 8- 3 √³82 +C

0 = 8-12 + C

C= 4

Rta: La función de ahorro total es S(Y) = Y –3 √³Y2 + 4.

Ejemplo 24 (Aplicación de la integral indefinida)

La propensión marginal al consumo es C’(Y) = 20 e-0.2Y. El gasto en consumo total es 60 cuando el ingreso es cero.

a-) Hallar la función de consumo.

Solución:

C(Y) = ∫ C´(Y) * dY

= ∫ (20 e-0.2Y) dY

= -20/ 0.2e-0.2y + C

C(0) = -100/e-0.2*0 +C

60 = -100+ C

C = 160

Rta: La función de consumo está dada por la expresión C(Y) = -20/ 0.2e-0.2y +160.

http://www.eumed.net/libros-gratis/2008a/363/CONSUMO%20Y%20AHORRO.htm

4.6 Diferenciales

Sea f(x) una función derivable. Diferencial de una función correspondiente al incremento h de la variable independiente, es el producto f'(x) · h. Se representa por dy.

La diferencial en un punto representa el incremento de la ordenada de la tangente, correspondiente a un incremento de la variable independiente.

Ejemplos

3. Calcular el incremento del área del cuadrado de 2 m de lado, cuando aumentamos 1 mm su lado.

S = x ²dS = 2x dx

d(S)= 2·2· 0.001 = 0.004 m²